Differentieller Interferenzkontrast
- Grundbegriffe & Prinzip

Die nachfolgenden Begriffe und Zusammenhänge sind fundamental für das Verständnis des DIK. Man sollte sich deshalb zunächst mit diesen Grundlagen vertraut machen.

	Licht als Wellenbewegung - wichtige Zusammenhänge

Kohärenz

Lichtwellen, die die nachfolgenden Kriterien erfüllen, werden als kohärent bezeichnet:

• gleiche Wellenlänge
• die Wellen schwingen in der gleichen Ebene
• zwischen den Wellen muss eine feste Phasenbeziehung bestehen

Wird Licht, das von einem Punkt einer Glühlampe ausgeht, in zwei Anteile aufgetrennt so sind die entstehenden Wellenzüge kohärent.

Interferenz

Kohärente Wellenzüge können sich zu einer neuen Lichtwelle vereinigen. Diese Erscheinung trägt die Bezeichnung Interferenz. Die Amplitude der resultierenden Welle wird dabei durch die Amplituden der interferierenden Partner sowie deren Phasenbeziehungen bestimmt und ergibt sich durch die geometrische Addition (Vektoraddition) der Amplituden der interferierenden Wellenzüge.

Zur Verdeutlichung wird nachfolgend das Ergebnis der Interferenz bei unterschiedlichen Phasenbeziehungen der interferierenden Wellen genauer betrachtet.

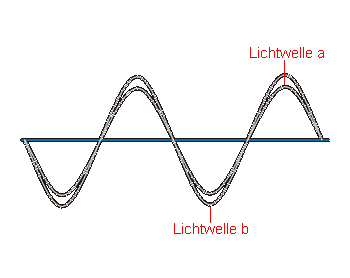
	Interferierende Wellen sind phasengleich
Sind die interferierenden Wellen phasengleich, so kommt es zu einer maximalen Verstärkung durch die Interferenz (konstruktive Interferenz).

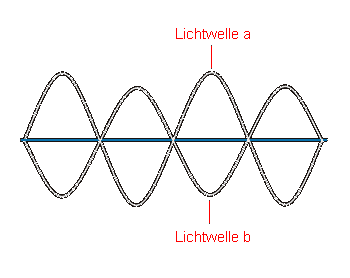
	Interferierende Wellen sind um 1/2 Wellenlänge verschoben
Beträgt die Phasendifferenz der interferierenden Partner 1/2 Wellenlänge, so kommt es zu einer maximalen Abschwächung durch die Interferenz (destruktive Interferenz). Wenn beide Wellen die gleiche Amplitude besitzen, so löschen sie sich gegenseitig völlig aus.

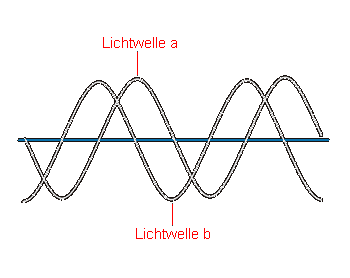
	Interferierende Wellen sind um 1/4 Wellenlänge verschoben
Beträgt die Phasendifferenz der interferierenden Partner etwa 1/4 Wellenlänge, so ergibt sich durch die Interferenz eine Lichtwelle von "mittlerer" Amplitude.

Man sollte sich den folgenden Sachverhalt einprägen:

Befinden sich die Lichtwellen auf der gleichen Phase, so ist eine maximale Verstärkung festzustellen, besteht jedoch eine Phasendifferenz von einer halben Wellenlänge, so besitzt der entstehende Wellenzug nur noch eine geringe Amplitude bis hin zur völligen Auslöschung bei gleicher Amplitude der interferierenden Wellenzüge. Zwischen diesen beiden Extremfällen entstehen durch die Interferenz "mittlere" Amplituden, die sich je nach Phasendifferenz den beiden beschriebenen Extremfällen annähern.

Phasendifferenz & Gangunterschied

Bei den obigen Beispielen zur Interferenz haben wir die Phasendifferenz zwischen zwei interferierenden Lichtwellen untersucht. Man kann den "Vorsprung" einer Lichtwelle im Vergleich zu einer zweiten Lichtwelle aber aber auch in Längeneinheiten angeben. Man spricht dann vom Gangunterschied und gibt diesen meist in nm oder µm an.
Rotes Licht hat beispielsweise eine Wellenlänge von 700 nm. Bei einer Phasendifferenz von 1/2 Wellenlänge beträgt der Gangunterschied folglich 350 nm.

Optische Weglänge

Medien mit hohem Lichtbrechungsindex wirken bremsend auf das Licht. Um die gleiche geometrische Weglänge zurückzulegen braucht deshalb Licht in einem Medium mit höherem Brechungsindex mehr Zeit, als in einem Medium mit geringerem Lichtbrechungsindex. Dieser Umstand wird durch die so genannte Optische Weglänge beschrieben.

	Das Prinzip des Differentiellen Interferenzkontrasts (I)
Nachdem wir die notwendigen Grundbegriffe zum Verständnis des DIK gelernt haben, ist es jetzt auch möglich das hinter dem Differentiellen Interferenzkontrast stehende Prinzip nachzuvollziehen. Die Wellenzüge des Mikroskopierlichts werden vor dem Präparat in zwei kohärente Anteile gleicher Amplitude aufgespalten. Je nach Präparatsituation (Lichtbrechungsindex) wird die optische Weglänge für beide Wellenzüge modifiziert und damit unterschiedlich ausfallen. Oberhalb des Präparates erfolgt die Wiedervereinigung der Teilwellen und es kommt zur Interferenz. Aus der unterschiedlichen optischen Weglänge der interferierenden Partner ergeben sich helle und dunkle Bereiche, die zu dem charakteristischen Relief-Effekt des DIK führen. Man spricht übrigens vom Differentiellen Interferenzkontrast, weil der horizontale Abstand zwischen den beiden Wellenzügen im Präparat so gering ist, dass er unter der Auflösungsgrenze des Mikroskops liegt. Wäre der Abstand größer, so könnte man im Mikroskop jede Präparatstruktur doppelt sehen. Amöbe im DIK mit dem typischen Relief-Kontrast durch Hell-Dunkel-Effekt

© 2001 Christian Linkenheld