Wichtige optische Bauelemente eines Mikroskops für den Differentiellen Interferenzkontrast

Die beschriebene Aufspaltung des Mikroskopierlichts für den DIK erfolgt auf polarisationsoptischem Weg. Nachfolgend werden die hierzu erforderlichen Bauelemente kurz beschrieben und dann noch zu einem vereinfachten Mikroskop für DIK zusammengefügt.

Die Darstellung ist nicht in allen Punkten exakt. Im Vordergrund steht die Frage nach der Aufgabe der optischen Bauelemente im Strahlengang des DIK ("Wer macht was?"). Auf das genaue "Wie" kann hier nicht näher eingegangen werden.

Natürliches Licht & linear polarisiertes Licht

Im natürlichen Licht treten alle Schwingungsebenen senkrecht zur Ausbreitungsrichtung auf. Im linear polarisierten Licht dagegen finden sich nur Lichtwellen, die in einer einzigen, ebenfalls senkrecht zur Ausbreitungsrichtung orientierten Ebenen schwingen.

Natürliches unpolarisiertes Licht Linear polarisiertes Licht

Der Polarisator

Man kann linear polarisiertes Licht durch spezielle Polarisationsfilter aus natürlichem Licht "erzeugen". Derartige Filter lassen lediglich den Anteil des Lichts hindurch, der parallel zur Durchlaßrichtung des Polarisators orientiert ist.

Man kann die Wirkung eines Polarisators auf Lichtwellen graphisch darstellen.

	Wirkung eines Polarisationsfilters auf Lichtwellen (I)
Lichtwelle schwingt in der Durchlaßrichtung Lichtwelle schwingt senkrecht zur Durchlaßrichtung Lichtwelle schwingt in einem Winkel von 45° zur Durchlaßrichtung => die Lichtwelle wird nicht beeinflusst => völlige Absorption der Lichtwelle => Schwächung der Amplitude & Drehung der  Schwingungsrichtung

	Wirkung eines Polarisationsfilters auf Lichtwellen (II)

Der Analysator

Bringt man nach dem Polarisator einen zweiten Polarisationsfilter in den Strahlengang, dessen Durchlaßrichtung senkrecht zu der des Polarisators orientiert ist (= Kreuzstellung), so wird das zuvor erzeugte linear polarisierte Licht durch diesen zweiten Filter völlig absorbiert. Dies ist leicht nachvollziehbar, da das Licht, welches den zweiten Filter erreicht, genau senkrecht zu dessen Durchlaßrichtung schwingt. Im Strahlengang des Mikroskops bezeichnet man diesen zweiten Polarisationsfilter als Analysator.

	Kombination aus Polarisator und Analysator

Die Bezeichnung "Analysator" kommt ursprünglich daher, dass man mit einem Pol-Filter nicht nur linear polarisiertes Licht erzeugen, sondern auch nachweisen und analysieren kann. Mit einem Polarisationsfilter kann man nämlich erkennen, ob Licht linear polarisiert ist und wie die Schwingungsebene des polarisierten Lichts orientiert ist. Dreht man ein Pol-Filter und nimmt abwechselnd Helligkeit und Dunkelheit wahr, so liegt linear polarisiertes Licht vor und bei Auftreten von Dunkelheit ist die Durchlaßrichtung des Analysators senkrecht zur Durchlaßrichtung des Filters orientiert, der das linear polarisierte Licht erzeugt hat.

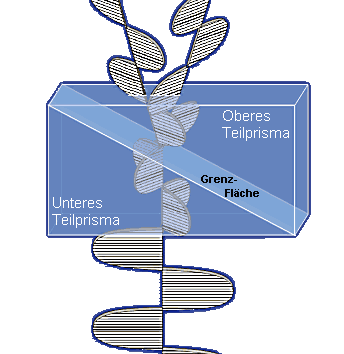
Das Wollaston-Prisma

Ein Wollaston-Prisma ist aus zwei Teilprismen aufgebaut, die aus Kalkspat oder Quarz bestehen und miteinander verkittet sind. Diagonal durch das Wollaston-Prisma verläuft die Grenzfläche zwischen diesen beiden Prismen.

Bei einer bestimmten Orientierung ist ein Wollaston-Prisma in der Lage linear polarisiertes Licht in zwei Wellenzüge gleicher Amplitude aufzuspalten. Da dies auf polarisationsoptischem Weg erfolgt wird dieses Prisma auch als Polarisations-Strahlteiler bezeichnet.

Im unteren Teilprisma wird der linear polarisierte Wellenzug in zwei Teilwellen gleicher Amplitude aufgespalten. Die Schwingungsebenen beider, wiederum polarisierten, Wellenzüge bilden hierbei einen rechten Winkel. An der Grenzfläche im Wollaston-Prisma teilen sich beide Wellen und divergieren.

	Das Wollaston-Prisma in der Funktion als Strahlteiler

Man kann durch ein zweites Wollaston-Prisma die beiden divergierenden Wellenzüge auch wieder zusammenbringen. Hierbei bleiben aber die senkrecht zu einander orientierten Schwingungsebenen unbeeinflusst.

Die Einzelprismen des Wollaston-Prismas besitzen die Eigenschaft der Doppelbrechung. Dies bedeutet unter anderem, dass der Lichtbrechungsindex für die beiden entstandenen Teilstrahlen unterschiedlich groß ist.

Im nachfolgenden Beispiel ist der Lichtbrechungsindex im unteren Prisma für den Teilstrahl 1 größer als für den Teilstrahl 2. Im oberen Prisma sind die Verhältnisse genau umgekehrt. Daraus ergibt sich, dass der Teilstrahl 1 im unteren Prisma im Vergleich zum anderen Strahl gebremst wird (größere optische Weglänge). Im oberen Prisma herrschen wiederum die umgekehrten Verhältnisse und Teilstrahl 2 wird stärker gebremst. Erfolgt die Trennung beider Teilstrahlen genau in der Mitte des Wollaston-Prismas (gleich Dicke der Teilprismen), so heben sich die unterschiedlichen optischen Weglängen gegenseitig auf und beide Teilstrahlen verlassen das Prisma ohne Gangunterschied.

	Wollaston-Prisma: Erzeugung eines Gangunterschiedes

Man kann einen linear polarisierten Lichtstrahl mit einem Wollaston-Prisma in zwei Teilstrahlen aufspalten und diese wieder mit einem zweiten Prisma zusammenführen. Gleichzeitig ist es möglich durch das Verschieben eines Wollaston-Prismas einen variablen Gangunterschied zwischen den Teilstrahlen zu erzeugen. Von diesen Fähigkeiten des Wollaston-Prismas wird im DIK Gebrauch gemacht.

	Das Grundprinzip des Differentiellen Interferenzkontrasts (II)
Mit dem Polarisator, dem Analysator, sowie dem Wollaston-Prisma haben wir die wichtigsten Bauteile, durch die ein Mikroskop für den Differentiellen Interferenzkontrast erweitert wird, kennen gelernt. Der Polarisationsfilter erzeugt linear polarisiertes Licht. Jeder Wellenzug dieses linear polarisierten Lichts wird durch ein Wollaston-Prisma in zwei Wellenzüge gleicher Amplitude aufgespalten. Die Schwingungsebenen dieser beiden Wellenzüge stehen senkrecht aufeinander. Durch ein zweites Wollaston-Prisma oberhalb des Präparates werden beide Wellenzüge räumlich wieder zusammengeführt. Sie schwingen aber nach wie vor in zwei unterschiedlichen Ebenen und sind somit nicht kohärent und interferenzfähig. Im Analysator werden die Schwingungsebenen dann zu dessen Durchlaßrichtung hin gedreht. Danach sind beide Teilwellen kohärent und vereinigen sich durch Interferenz zu einem einzigen Wellenzug. Die Amplitude (Helligkeit) dieses Wellenzugs wird durch die Phasenbeziehungen der interferierenden Partner bestimmt. Beide Teilwellen durchlaufen das Präparat an unterschiedlichen Stellen. In einem Präparat ändert sich jedoch der Lichtbrechungsindex und damit die optische Weglänge stetig (z.B. zwischen Zellkern und umgebenden Zellplasma). Das Ergebnis der Interferenz gibt somit die unterschiedliche Modifizierung der optischen Weglänge beider Teilwellen durch das Präparat wieder. Amöbe im DIK mit dem typischen Relief-Kontrast durch Hell-Dunkel-Effekt

© 2001 Christian Linkenheld